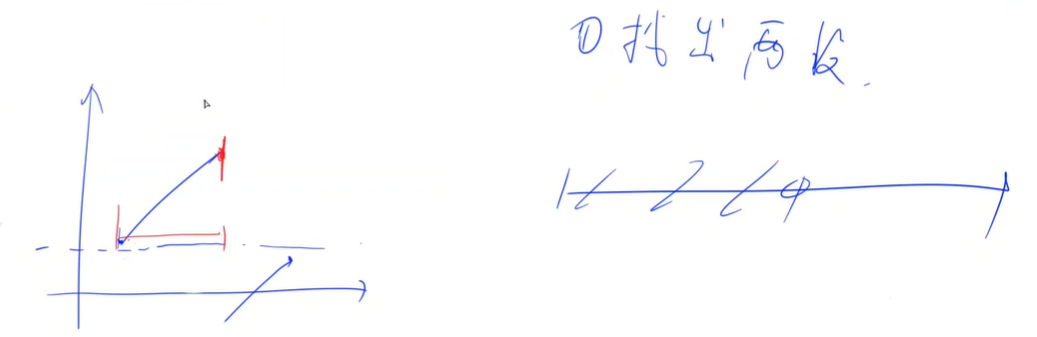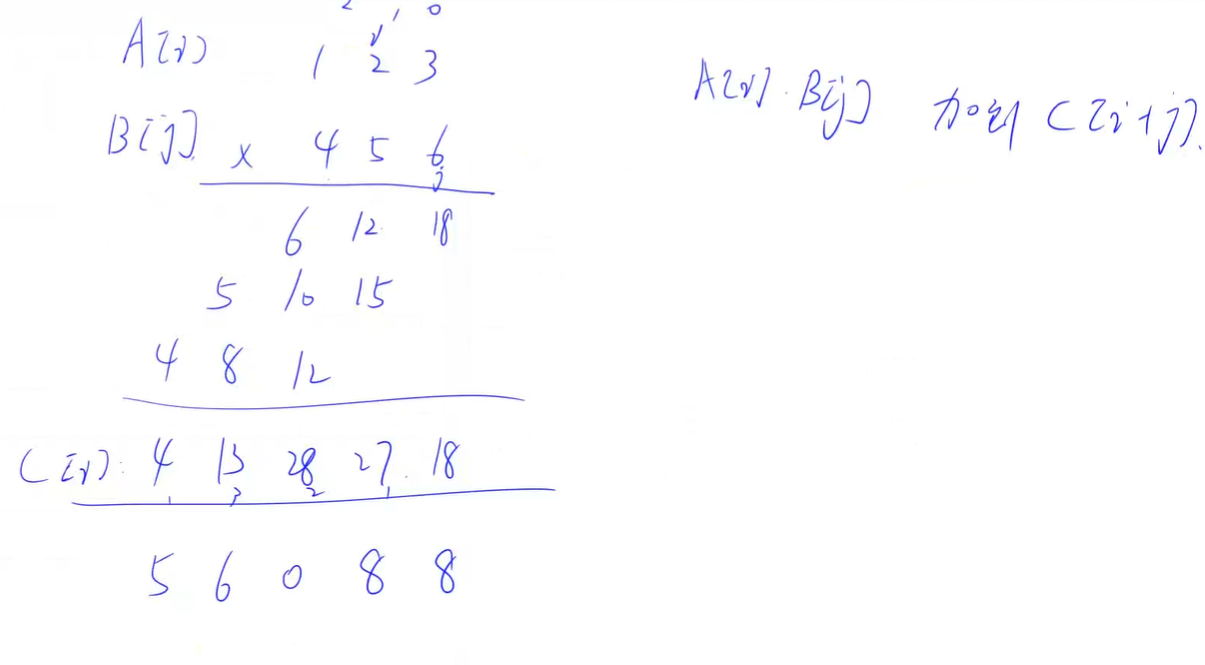郭霖的博客

腾讯音乐实习ing

LeedCode

发表于 更新于 分类于
本文字数： 60k 阅读时长 ≈ 55 分钟

1. 两数之和

两数之和

思路：
用哈希表储存已经遍历过的值，再通过int r = target - nums[i];查看哈希表中是否存在一个值，与nums[i]之和为target

时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> hashmap;
        for (int i = 0; i < nums.size(); i++) {
            int tmp = target - nums[i];
            if (hashmap.count(tmp)) {
                return {hashmap[tmp], i};
            } else {
                hashmap[nums[i]] = i;
            }
        }
        return {};
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <vector>
#include <unordered_map>

using namespace std;

vector<int> twoSum(vector<int>& nums, int target) {
    unordered_map<int, int> hash;
    for (int i = 0; i < nums.size(); i++) {
        int r = target - nums[i];
        if (hash.count(r)) {
            return {i, hash[r]};
        } else {
            hash[nums[i]] = i;
        }
    }
    return {};
}

int main() {
    vector<int> ans;
    vector<int> nums = {2, 7, 11, 15};
    int target = 9;
    ans = twoSum(nums, target);
    for (int i : ans) {
        cout << i << endl;
    }
    return 0;
}

2. 两数相加

两数相加

思路：
遍历一遍即可，注意进位
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        // 虚拟头节点
        auto dummy = new ListNode(-1);
        // 当前尾节点位置
        auto cur = dummy;
        int t = 0;
        while (l1 && l2) {
            t = l1->val + l2->val + t;
            auto p = new ListNode(t % 10);
            t /= 10;
            cur->next = p;
            cur = cur->next;
            // 节点向后移
            l1 = l1->next;
            l2 = l2->next;
        }

        while (l1) {
            t = l1->val + t;
            auto p = new ListNode(t % 10);
            t /= 10;
            cur->next = p;
            cur = cur->next;
            // 节点向后移
            l1 = l1->next;
        }

        while (l2) {
            t = l2->val + t;
            auto p = new ListNode(t % 10);
            t /= 10;
            cur->next = p;
            cur = cur->next;
            // 节点向后移
            l2 = l2->next;
        }

        // 看看最后是否还有进位
        if (t) {
            auto p = new ListNode(t);
            cur->next = p;
            cur = cur->next;
        }

        return dummy->next;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include <iostream>
#include <vector>

using namespace std;

// 定义链表的节点规则
struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
    // 虚拟头节点
    auto dummy = new ListNode(-1);
    // 当前尾节点位置
    auto cur = dummy;
    int t = 0;
    while (l1 && l2) {
        t = l1->val + l2->val + t;
        auto p = new ListNode(t % 10);
        t /= 10;
        cur->next = p;
        cur = cur->next;
        // 节点向后移
        l1 = l1->next;
        l2 = l2->next;
    }

    while (l1) {
        t = l1->val + t;
        auto p = new ListNode(t % 10);
        t /= 10;
        cur->next = p;
        cur = cur->next;
        // 节点向后移
        l1 = l1->next;
    }

    while (l2) {
        t = l2->val + t;
        auto p = new ListNode(t % 10);
        t /= 10;
        cur->next = p;
        cur = cur->next;
        // 节点向后移
        l2 = l2->next;
    }

    // 看看最后是否还有进位
    if (t) {
        auto p = new ListNode(t);
        cur->next = p;
        cur = cur->next;
    }

    return dummy->next;
}

int main() {
    int n;
    // 构造第一个链表，输入-1时停止
    auto dummy1 = new ListNode(-1);
    auto cur1 = dummy1;
    while (cin >> n, n != -1) {
        auto p = new ListNode(n);
        cur1->next = p;
        cur1 = cur1->next;
    }

    // 构造第二个链表，输入-1时停止
    auto dummy2 = new ListNode(-1);
    auto cur2 = dummy2;
    while (cin >> n, n != -1) {
        auto p = new ListNode(n);
        cur2->next = p;
        cur2 = cur2->next;
    }

    // 输出结果
    auto p = addTwoNumbers(dummy1->next, dummy2->next);
    for (auto i = p; i; i = i->next) {
        cout << i->val << ' ';
    }
    cout << endl;
    return 0;
}

3. 无重复字符的最长子串

无重复字符的最长子串

思路：
双指针算法 + 哈希表
利用指针i前进，同时哈希表统计是否有重复的字符。如果有重复字符，那么指针j也前进，直到重复字符消失为止，比较统计最大长度。
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
int lengthOfLongestSubstring(string s) {
    unordered_map<char, int> hash;
    int res = 0;
    for (int i = 0, j = 0; i < s.size(); i++) {
        hash[s[i]]++;
        while (hash[s[i]] > 1) {
            hash[s[j]]--;
            j++;
        }
        res = max(res, i - j + 1);
    }
    return res;
}

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
#include <unordered_map>

using namespace std;

int lengthOfLongestSubstring(string s) {
    unordered_map<char, int> hash;
    int res = 0;
    for (int i = 0, j = 0; i < s.size(); i++) {
        hash[s[i]]++;
        while (hash[s[i]] > 1) {
            hash[s[j]]--;
            j++;
        }
        res = max(res, i - j + 1);
    }
    return res;
}

int main() {
    string s;
    cin >> s;
    int len = lengthOfLongestSubstring(s);
    cout << len << endl;
    return 0;
}

4. 寻找两个正序数组的中位数

4. 寻找两个正序数组的中位数

时间复杂度：O(log (m+n))

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <bits/stdc++.h>

using namespace std;

// 相当于找两个数组的第k大的数
// i 是第一个数组起始的位置，j是第二个数组起始的位置
int find(vector<int>& nums1, int i, vector<int>& nums2, int j, int k) {
    // 让nums1长度小于nums2
    if (nums1.size() - i > nums2.size() - j) return find(nums2, j, nums1, i, k);

    // 如果nums1空了，就直接取nums2的中位数
    if (nums1.size() == i) return nums2[j + k - 1];

    // 如果只有一个元素了，就取两个数组的开头元素中最小的那个
    if (k == 1) {
        return min(nums1[i], nums2[j]);
    }

    // 每次筛掉小的那一段
    int si = min((int)nums1.size(), i + k / 2);
    int sj = j + k - k / 2;
    if (nums1[si - 1] < nums2[sj - 1]) {
        return find(nums1, si, nums2, j, k - si + i);
    } else return find(nums1, i, nums2, sj, k - sj + j);
}

double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
    int tot = nums1.size() + nums2.size();
    if (tot % 2 == 0) {
        // 相当于先找前tot / 2个数
        int left = find(nums1, 0, nums2, 0, tot / 2);
        // 找前tot / 2 + 1个数
        int right = find(nums1, 0, nums2, 0, tot / 2 + 1);
        return (left + right) / 2.0;
    } else return find(nums1, 0, nums2, 0, tot / 2 + 1);
}

int main() {
    vector<int> nums1 = {1,3}, nums2 = {4};
    cout << findMedianSortedArrays(nums1, nums2) << endl;
    return 0;
}

5. 最长回文子串

最长回文子串

思路：
分别考虑奇数回文子串和偶数回文子串即可
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
string longestPalindrome(string s) {
    int res = 0;
    string ans;
    // 找出最长的奇数回文子串
    for (int i = 0; i < s.size(); i++) {
        int l = i - 1, r = i + 1;
        while (l >= 0 && r < s.size() && s[l] == s[r]) {
            l--, r++;
        }
        if (res < r - l - 1) {
            res = r - l - 1;
            ans = s.substr(l + 1, res);
        }
    }

    // 找出最长的偶数回文子串
    for (int i = 0; i < s.size(); i++) {
        int l = i, r = i + 1;
        while (l >= 0 && r < s.size() && s[l] == s[r]) {
            l--, r++;
        }
        if (res < r - l - 1) {
            res = r - l - 1;
            ans = s.substr(l + 1, res);
        }
    }
    return ans;
}

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>

using namespace std;

string longestPalindrome(string s) {
    int res = 0;
    string ans;
    // 找出最长的奇数回文子串
    for (int i = 0; i < s.size(); i++) {
        int l = i - 1, r = i + 1;
        while (l >= 0 && r < s.size() && s[l] == s[r]) {
            l--, r++;
        }
        if (res < r - l - 1) {
            res = r - l - 1;
            ans = s.substr(l + 1, res);
        }
    }

    // 找出最长的偶数回文子串
    for (int i = 0; i < s.size(); i++) {
        int l = i, r = i + 1;
        while (l >= 0 && r < s.size() && s[l] == s[r]) {
            l--, r++;
        }
        if (res < r - l - 1) {
            res = r - l - 1;
            ans = s.substr(l + 1, res);
        }
    }
    return ans;
}


int main() {
    string s;
    cin >> s;
    cout << longestPalindrome(s) << endl;
    return 0;
}

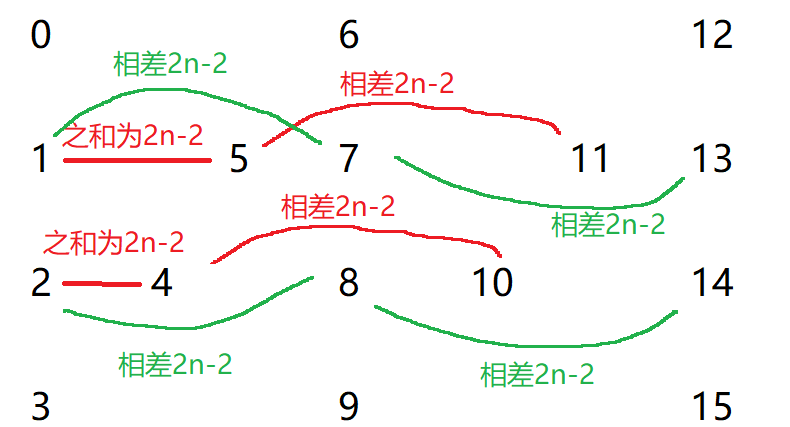
6. Z 字形变换

Z 字形变换

思路：
第一行和最后一行，每个数字之间间隔是2n-2：

在这里插入图片描述
中间行分2个队伍，分别向后相差2n-2，两个队伍的队头之和为2n-2：
在这里插入图片描述
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    string convert(string s, int n) {
        // 一行的时候直接返回s即可
        if (n == 1) return s;
        string ans;
        for (int i = 0; i < n; i++) {
            // 第一行和最后一行，每个数字之间间隔是2n - 2
            if (i == 0 || i == n - 1) {
                for (int j = i; j < s.size(); j += 2 * n - 2) {
                    ans += s[j];
                }
            } else {
                // 中间行分2个队伍j和k，分别向后相差2n-2，两个队伍的队头j和k之和为2n-2
                for (int j = i, k = 2 * n - 2 - j; j < s.size(); j += 2 * n - 2, k += 2 * n - 2) {
                    // j队伍在前
                    ans += s[j];
                    
                    // k队伍在后，总是一个j一个k，这样轮循下去
                    if (k < s.size()) {
                        ans += s[k];
                    }
                }
            }
        }
        return ans;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>

using namespace std;

string convert(string s, int n) {
    // 一行的时候直接返回s即可
    if (n == 1) return s;
    string ans;
    for (int i = 0; i < n; i++) {
        // 第一行和最后一行，每个数字之间间隔是2n - 2
        if (i == 0 || i == n - 1) {
            for (int j = i; j < s.size(); j += 2 * n - 2) {
                ans += s[j];
            }
        } else {
            // 中间行分2个队伍j和k，分别向后相差2n-2，两个队伍的队头j和k之和为2n-2
            for (int j = i, k = 2 * n - 2 - j; j < s.size(); j += 2 * n - 2, k += 2 * n - 2) {
                // j队伍在前
                ans += s[j];

                // k队伍在后，总是一个j一个k，这样轮循下去
                if (k < s.size()) {
                    ans += s[k];
                }
            }
        }
    }
    return ans;
}

int main() {
    string s;
    int n;
    cin >> s >>  n;
    cout << convert(s, n) << endl;
    return 0;
}

7. 整数反转

整数反转

思路：
将ans * 10 + res[i] 转化为 ans <= double (INT_MAX - res[i] - 1) / 10即可
时间复杂度：O($log10n$)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
	int reverse(int x) {
	    if (x == INT_MIN) return 0;
	    int ans = 0;
	    int sign = 1;
	    if (x < 0) {
	        sign = -1;
	        x = -x;
	    }
	    vector<int> res;
	    while (x) {
	        res.push_back(x % 10);
	        x /= 10;
	    }
	    for (int i = 0; i < res.size(); i++) {
	        if (ans <= double (INT_MAX - res[i]) / 10) {
	            ans = ans * 10 + res[i];
	        } else return 0;
	    }
	    ans *= sign;
	    return ans;
	}
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <vector>

using namespace std;

int reverse(int x) {
    int ans = 0;
    int sign = 1;
    if (x == INT_MIN) return 0;
    if (x < 0) {
        sign = -1;
        x = -x;
    }
    vector<int> res;
    while (x) {
        res.push_back(x % 10);
        x /= 10;
    }
    for (int i = 0; i < res.size(); i++) {
        if (ans <= double (INT_MAX - res[i]) / 10) {
            ans = ans * 10 + res[i];
        } else return 0;
    }
    ans *= sign;
    return ans;
}

int main() {
    int x;
    cin >> x;
    cout << reverse(x) << endl;
    return 0;
}

8. 字符串转换整数 (atoi)

字符串转换整数 (atoi)

思路：
细心点即可，小心超出long long 的范围
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int myAtoi(string s) {
        int k = 0;
        int sign = 1;
        long long ans = 0;
        // 丢弃无用的前导空格
        while (k < s.size() && s[k] == ' ') k++;

        // 检查下一个字符（假设还未到字符末尾）为正还是负号
        if (k < s.size() && s[k] == '-') k++, sign = -1;
        else if (k < s.size() && s[k] == '+') k++;

        for (int i = k; i < s.size(); i++) {
            if (ans > INT_MAX) break;
            if (s[i] >= '0' && s[i] <= '9') {
                ans = ans * 10 + s[i] - '0';
            } else {
                break;
            }
        }
        // 加符号
        ans *= sign;
        if (ans > INT_MAX) ans = INT_MAX;
        if (ans < INT_MIN) ans = INT_MIN;
        return ans;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>

using namespace std;

int myAtoi(string s) {
    int k = 0;
    int sign = 1;
    long long ans = 0;
    // 丢弃无用的前导空格
    while (k < s.size() && s[k] == ' ') k++;

    // 检查下一个字符（假设还未到字符末尾）为正还是负号
    if (k < s.size() && s[k] == '-') k++, sign = -1;
    else if (k < s.size() && s[k] == '+') k++;

    for (int i = k; i < s.size(); i++) {
        if (ans > INT_MAX) break;
        if (s[i] >= '0' && s[i] <= '9') {
            ans = ans * 10 + s[i] - '0';
        } else {
            break;
        }
    }
    // 加符号
    ans *= sign;
    if (ans > INT_MAX) ans = INT_MAX;
    if (ans < INT_MIN) ans = INT_MIN;
    return ans;
}

int main() {
    string s;
    cin >> s;
    cout << myAtoi(s) << endl;
    return 0;
}

9. 回文数

回文数

思路：
利用字符串转换函数to_string(x)和字符串翻转函数string(str.rbegin(), str.rend());
核心代码：

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    bool isPalindrome(int x) {
        if (x < 0) return false;
        string str = to_string(x);
        // 字符串翻转函数
        string str2 = string(str.rbegin(), str.rend());
        return str == str2;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <iostream>

using namespace std;

bool isPalindrome(int x) {
    if (x < 0) return false;
    string str = to_string(x);
    string str2 = string(str.rbegin(), str.rend());
    return str == str2;
}

int main() {
    int x;
    cin >> x;
    cout << isPalindrome(x) << endl;
    return 0;
}

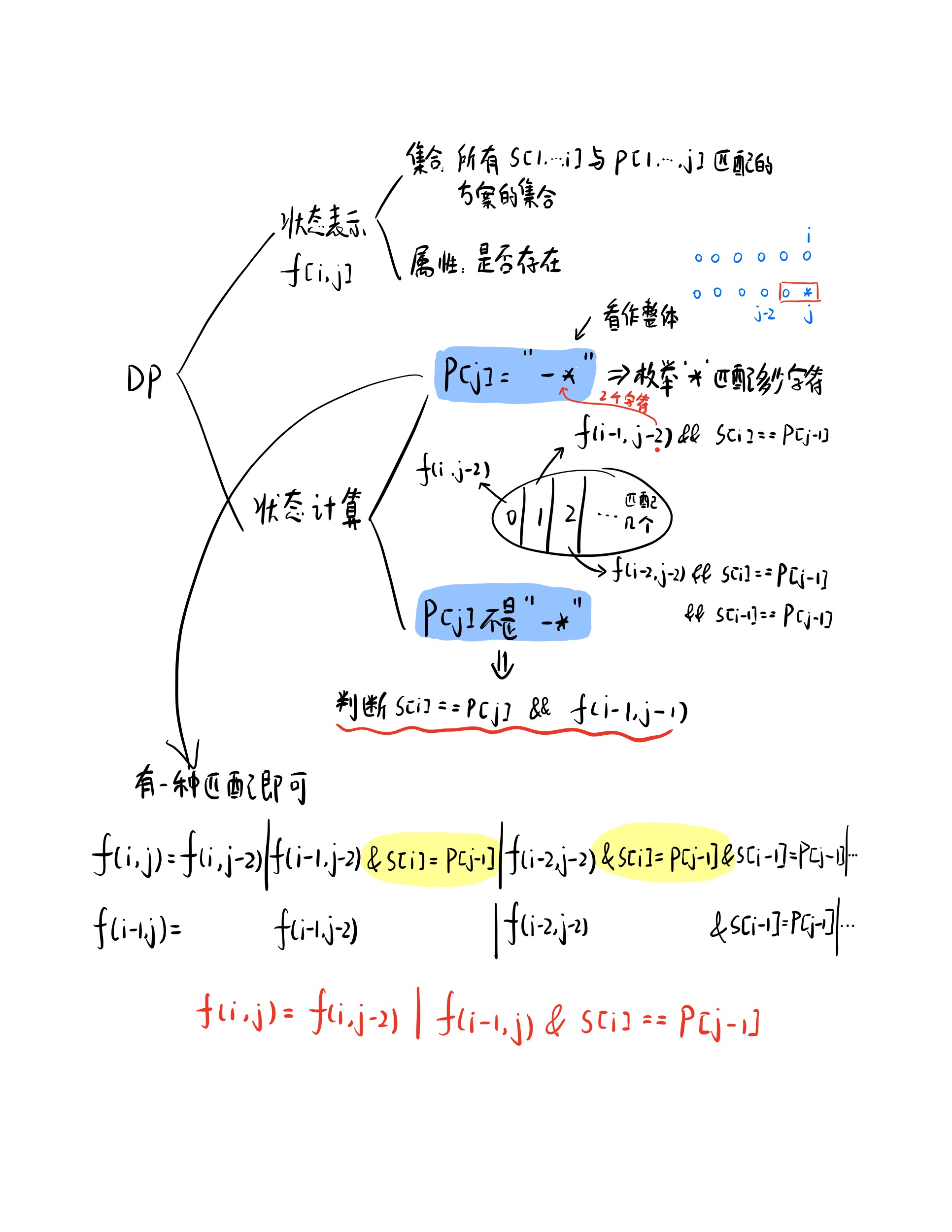
10. 正则表达式匹配

10. 正则表达式匹配

时间复杂度：O(n*m)

202208131754

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>

using namespace std;

bool isMatch(string s, string p) {
    int n = s.size(), m = p.size();
    // 下标从1开始
    s = ' ' + s, p = ' ' + p;
    vector<vector<bool>> f(n + 10, vector<bool>(m + 10));
    f[0][0] = true;

    // 第一个串为空时，可能匹配，因为'*' 可匹配零个，所以下标可从0开始
    for (int i = 0; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            // 当前位应该和下一位看作整体
            if (j + 1 <= m && p[j + 1] == '*') continue;

            if (i && p[j] != '*') f[i][j] = (s[i] == p[j] || p[j] == '.') && f[i - 1][j - 1];
            else if (p[j] == '*') {
                f[i][j] = f[i][j - 2] || i && f[i - 1][j] && (s[i] == p[j - 1] || p[j - 1] == '.');
            }
        }
    }
    return f[n][m];
}

int main() {
    string s, p;
    cin >> s >> p;
    cout << isMatch(s, p) << endl;
    return 0;
}

11. 盛最多水的容器

盛最多水的容器

思路：
假设左边先到达最优解，证明右边一定会向最优解靠拢
也就是说当左边到达最优解时，右边在最优解之前的值，一定都比左边的值要短，从而左边不动，右边向左靠拢，直到经过右边最优解为止
在这里插入图片描述
结论，只要左边先到达最优解，那么右边到达最优解之前的值，一定小于左边的最优解
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maxArea(vector<int>& height) {
        int l = 0, r = height.size() - 1;
        int ans = 0;
        while (l < r) {
            ans = max(ans, min(height[l], height[r]) * (r - l));
            if (height[l] < height[r]) l++;
            else r--;
        }
        return ans;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>
#include <vector>

using namespace std;

int maxArea(vector<int>& height) {
    int l = 0, r = height.size() - 1;
    int ans = 0;
    while (l < r) {
        ans = max(ans, min(height[l], height[r]) * (r - l));
        if (height[l] < height[r]) l++;
        else r--;
    }
    return ans;
}

int main() {
    vector<int> height = {1,8,6,2,5,4,8,3,7};
    cout << maxArea(height) << endl;
    return 0;
}

12. 整数转罗马数字

整数转罗马数字

核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    string intToRoman(int num) {
        int valus[] = {
            1000,
            900, 500, 400, 100,
            90, 50, 40, 10,
            9, 5, 4, 1
        };
        string reps[] = {
            "M",
            "CM", "D", "CD", "C",
            "XC", "L", "XL", "X",
            "IX", "V", "IV", "I"
        };

        string res;
        for (int i = 0; i <= 12; i++) {
            while (num >= valus[i]) {
                num -= valus[i];
                res += reps[i];
            }
        }
        return res;
    }
};

13. 罗马数字转整数

罗马数字转整数

核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int romanToInt(string s) {
        unordered_map<char, int> hash;
        hash['I'] = 1, hash['V'] = 5;
        hash['X'] = 10, hash['L'] = 50;
        hash['C'] = 100, hash['D'] = 500;
        hash['M'] = 1000;

        int res = 0;
        for (int i = 0; i < s.size(); i++) {
            if (i + 1 < s.size() && hash[s[i]] < hash[s[i + 1]]) {
                res -= hash[s[i]];
            } else {
                res += hash[s[i]];
            }
        }
        return res;
    }
};

14. 最长公共前缀

最长公共前缀

思路：
把最短的字符串放在第一个，然后逐位和后面的字符串相应位置比较，如果遇到不同的直接跳出双重循环
时间复杂度：O(nn)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        if (strs.size() == 1) return strs[0];

        // 找到长度最短的字符串
        int minv = strs[0].size();
        // 长度最短的字符串的下标
        int idx = 0;
        for (int i = 1; i < strs.size(); i++) {
            if (strs[i].size() < minv) {
                minv = strs[i].size();
                idx = i;
            }
        }

        if (idx) swap(strs[0], strs[idx]);

        int res = 0;

        bool sign = false;
        
        for (int i = 0; i < strs[0].size(); i++) {
            for (int j = 1; j < strs.size(); j++) {
                if (strs[j][i] != strs[0][i]) {
                    sign = true;
                    break;
                }
                if (j == strs.size() - 1) res++;
            }
            if (sign) break;
        }
        return strs[0].substr(0, res);
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
#include <vector>

using namespace std;

string longestCommonPrefix(vector<string>& strs) {
    if (strs.size() == 1) return strs[0];

    // 找到长度最短的字符串
    int minv = strs[0].size();
    // 长度最短的字符串的下标
    int idx = 0;
    for (int i = 1; i < strs.size(); i++) {
        if (strs[i].size() < minv) {
            minv = strs[i].size();
            idx = i;
        }
    }

    if (idx) swap(strs[0], strs[idx]);

    int res = 0;

    bool sign = false;

    for (int i = 0; i < strs[0].size(); i++) {
        for (int j = 1; j < strs.size(); j++) {
            if (strs[j][i] != strs[0][i]) {
                sign = true;
                break;
            }
            if (j == strs.size() - 1) res++;
        }
        if (sign) break;
    }
    return strs[0].substr(0, res);
}

int main() {
    vector<string> strs = {"cir","car"};
    cout << longestCommonPrefix(strs) << endl;
    return 0;
}

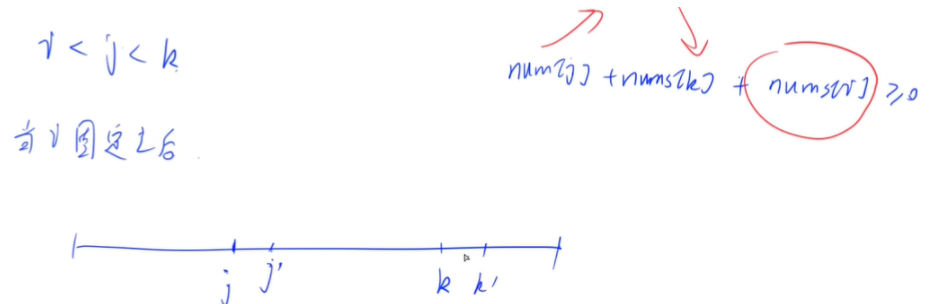
15. 三数之和

三数之和

思路：
算法：排序+双指针
先排序，然后固定i，然后j和k相互靠拢
双指针做法，首先想暴力做法怎么做，然后看是否有单调性，有单调性可以考虑双指针，双指针可以优化掉一个次方的时间复杂度，从n3优化到n2
而且j越大，k一定越小，这一点就保证了j和k一次最多只扫描了n，当j越大，k已经没必要从最右边开始扫描了，只需要从之前的地方往左就行，因为nums[j]增加，nums[k]必须不变或者变小，才有意义
在这里插入图片描述
题目要求不能有重复，如果nums[i]和等于nums[i - 1]的话，那么nums[i]的所有j和k，其实在nums[i - 1]已经全部枚举完了，所以得去除nums[i]==nums[i - 1]的j和k，也就是跳过，一直到nums[i]和前面不一样才行
在这里插入图片描述
因为是有序的，如果三元组的第一个数不一样，后面肯定不一样
然后当i相同时，nums[j]也不能等于nums[j - 1]

时间复杂度：O(n2)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> ans;
        if (nums.size() < 3) return ans;
        sort(nums.begin(), nums.end());
        for (int i = 0; i < nums.size(); i++) {
            if (i && nums[i] == nums[i - 1]) continue;
            for (int j = i + 1, k = nums.size() - 1; j < k; j++) {
                if (j > i + 1 && nums[j] == nums[j - 1]) continue;
                while (j < k - 1 && nums[i] + nums[j] + nums[k - 1] >= 0) k--;
                if (nums[i] + nums[j] + nums[k] == 0) {
                    ans.push_back({nums[i], nums[j], nums[k]});
                }
            }
        }
        return ans;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector<vector<int>> threeSum(vector<int>& nums) {
    vector<vector<int>> ans;
    if (nums.size() < 3) return ans;
    sort(nums.begin(), nums.end());
    for (int i = 0; i < nums.size(); i++) {
        if (i && nums[i] == nums[i - 1]) continue;
        for (int j = i + 1, k = nums.size() - 1; j < k; j++) {
            if (j > i + 1 && nums[j] == nums[j - 1]) continue;
            while (j < k - 1 && nums[i] + nums[j] + nums[k - 1] >= 0) k--;
            if (nums[i] + nums[j] + nums[k] == 0) {
                ans.push_back({nums[i], nums[j], nums[k]});
            }
        }
    }
    return ans;
}

int main() {
    vector<int> nums = {-1,0,1,2,-1,-4};
    vector<vector<int>> ans = threeSum(nums);
    for (int i = 0; i < ans.size(); i++) {
        for (int j = 0; j < ans[0].size(); j++) {
            cout << ans[i][j] << ' ';
        }
        cout << endl;
    }
    cout << endl;
    return 0;
}

16. 最接近的三数之和

最接近的三数之和

思路一：
暴力解法
时间复杂度：O(n3)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
	int threeSumClosest(vector<int>& nums, int target) {
	    int minv = INT_MAX;
	    int sum = 0;
	    int minSum = 0;
	    for (int i = 0; i < nums.size(); i++) {
	        for (int j = i + 1, k = nums.size() - 1; j < k; j++) {
	            while (j < k) {
	                sum = nums[i] + nums[j] + nums[k];
	                if (minv > abs(sum - target)) {
	                    minSum = sum;
	                    minv = abs(sum - target);
	                    if (minv == 0) return minSum;
	                }
	                k--;
	            }
	            k = nums.size() - 1;
	        }
	    }
	    return minSum;
	}
};

思路二：
排序+双指针优化掉一重循环
首先将 nums 数组排序，然后固定一重循环枚举起始位置 i ，这样就优化成 2 个数 j, k 之和最接近 target 的问题了
然后初始 j = i + 1, k = nums.size() - 1；如果发现 sum == target，则可以直接返回 target
若发现 sum < target，则 j++；否则 k–，这样就会向 target 逼近
直到 j >= k 停止，继续向后增加初始位置 i
时间复杂度：O(n2)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
	int threeSumClosest(vector<int>& nums, int target) {
	    sort(nums.begin(), nums.end());
	    int minv = INT_MAX;
	    int sum = 0;
	    int minSum = 0;
	    for (int i = 0; i < nums.size(); i++) {
	        int j = i + 1, k = nums.size() - 1;
	        while (j < k) {
	            sum = nums[i] + nums[j] + nums[k];
	            if (minv > abs(sum - target)) {
	                minSum = sum;
	                minv = abs(sum - target);
	            }
	            if (sum == target) return target;
	            else if (sum < target) j++;
	            else k--;
	        }
	    }
	    return minSum;
	}
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int threeSumClosest(vector<int>& nums, int target) {
    sort(nums.begin(), nums.end());
    int minv = INT_MAX;
    int sum = 0;
    int minSum = 0;
    for (int i = 0; i < nums.size(); i++) {
        int j = i + 1, k = nums.size() - 1;
        while (j < k) {
            sum = nums[i] + nums[j] + nums[k];
            if (minv > abs(sum - target)) {
                minSum = sum;
                minv = abs(sum - target);
            }
            if (sum == target) return target;
            else if (sum < target) j++;
            else k--;
        }
    }
    return minSum;
}

int main() {
    vector<int> nums = {0,1,1,1};
    int target = -100;
    cout << threeSumClosest(nums, target) << endl;
    return 0;
}

17. 电话号码的字母组合

电话号码的字母组合

思路：
递归
时间复杂度：O(4n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    string str[10] = {
            "", "", "abc", "def",
            "ghi", "jkl", "mno",
            "pqrs", "tuv", "wxyz"
    };

    vector<string> ans;

    void dfs(string &digits, int u, string path) {
        if (u == digits.size()) {
            ans.push_back(path);
            return;
        }
        int k = digits[u] - '0';
        for (int i = 0; i < str[k].size(); i++) {
            dfs(digits, u + 1, path + str[k][i]);
        }
    }

    vector<string> letterCombinations(string digits) {
        if (digits.size() == 0) return {};
        int u = 0;
        string path;
        dfs(digits, u, path);
        return ans;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
#include <vector>

using namespace std;

string str[10] = {
        "", "", "abc", "def",
        "ghi", "jkl", "mno",
        "pqrs", "tuv", "wxyz"
};

vector<string> ans;

void dfs(string &digits, int u, string path) {
    if (u == digits.size()) {
        ans.push_back(path);
        return;
    }
    int k = digits[u] - '0';
    for (int i = 0; i < str[k].size(); i++) {
        dfs(digits, u + 1, path + str[k][i]);
    }
}

vector<string> letterCombinations(string digits) {
    if (digits.size() == 0) return {};
    int u = 0;
    string path;
    dfs(digits, u, path);
    return ans;
}

int main() {
    string s;
    cin >> s;
    vector<string> ans = letterCombinations(s);
    for (string i : ans) {
        cout << i << ' ';
    }
    cout << endl;
    return 0;
}

18. 四数之和

四数之和

思路：
排序+双指针优化一层复杂度
注意爆 int ，要用 long long 存储四数之和
时间复杂度：O(n3)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> ans;
        sort(nums.begin(), nums.end());
        for (int i = 0; i < nums.size(); i++) {
            if (i && nums[i] == nums[i - 1]) continue;
            for (int j = i + 1; j < nums.size(); j++) {
                if (j > i + 1 && nums[j] == nums[j - 1]) continue;
                for (int k = j + 1, u = nums.size() - 1; k < u; k++) {
                    if (k > j + 1 && nums[k] == nums[k - 1]) continue;
                        while (k < u - 1 && (long long) nums[i] + nums[j] + nums[k] + nums[u - 1] - target >= 0) u--;
                        if ((long long) nums[i] + nums[j] + nums[k] + nums[u] == target) {
                            ans.push_back({nums[i], nums[j], nums[k], nums[u]});
                        }
                }
            }
        }
        return ans;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector<vector<int>> fourSum(vector<int>& nums, int target) {
    vector<vector<int>> ans;
    sort(nums.begin(), nums.end());
    for (int i = 0; i < nums.size(); i++) {
        if (i && nums[i] == nums[i - 1]) continue;
        for (int j = i + 1; j < nums.size(); j++) {
            if (j > i + 1 && nums[j] == nums[j - 1]) continue;
            for (int k = j + 1, u = nums.size() - 1; k < u; k++) {
                if (k > j + 1 && nums[k] == nums[k - 1]) continue;
                    while (k < u - 1 && nums[i] + nums[j] + nums[k] + nums[u - 1] - target >= 0) u--;
                    if ((long long) nums[i] + nums[j] + nums[k] + nums[u] == target) {
                        ans.push_back({nums[i], nums[j], nums[k], nums[u]});
                    }
            }
        }
    }
    return ans;
}

int main() {
    vector<int> nums = {1,0,-1,0,-2,2};
    int target = 0;
    vector<vector<int>> ans = fourSum(nums, target);
    for (int i = 0; i < ans.size(); i++) {
        for (int j = 0; j < ans[i].size(); j++) {
            cout << ans[i][j] << ' ';
        }
        cout << endl;
    }
    cout << endl;
    return 0;
}

19. 删除链表的倒数第 N 个结点

删除链表的倒数第 N 个结点

思路：
遍历一遍统计节点个数，在遍历一遍删除对应节点
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        auto dummy = new ListNode(-1);
        dummy->next = head;
        int i = 0;
        // 统计链表总共有多少个节点
        for (auto p = dummy->next; p; p = p->next) {
            i++;
        }
        int j = i - n;
        auto cur = dummy;
        while (j--) {
            cur = cur->next;
        }
        cur->next = cur->next->next;
        return dummy->next;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>

using namespace std;

// 定义链表节点的结构体
struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

// 删除链表的倒数第 N 个结点
ListNode* removeNthFromEnd(ListNode* head, int n) {
    auto dummy = new ListNode(-1);
    dummy->next = head;
    int i = 0;
    // 统计链表总共有多少个节点
    for (auto p = dummy->next; p; p = p->next) {
        i++;
    }
    int j = i - n;
    auto cur = dummy;
    while (j--) {
        cur = cur->next;
    }
    cur->next = cur->next->next;
    return dummy->next;
}

// 测试样例
int main() {
    int k;
    auto dummy = new ListNode(-1);
    auto cur = dummy;
    while (cin >> k, k != -1) {
        cur->next = new ListNode(k);
        cur = cur->next;
    }
    int n;
    cin >> n;
    auto head = removeNthFromEnd(dummy->next, n);
    for (auto i = head; i; i = i->next) {
        cout << i->val << ' ';
    }
    cout << endl;
    return 0;
}

20. 有效的括号

有效的括号

思路：
用栈，如果是左括号，就压栈，然后continue
如果是右括号，则看栈顶是不是对应的左括号，如果不是，则压栈
如果是右括号，栈为空，则返回false
如果遍历完毕，栈为空则返回true，否则返回false
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    stack<char> stk;
    bool isValid(string s) {
        for (int i = 0; i < s.size(); i++) {
            if (s[i] == '(' || s[i] == '[' || s[i] == '{') {
                stk.push(s[i]);
                continue;
            }

            if (stk.empty() && (s[i] == ')' || s[i] == ']' || s[i] == '}')) return false;

            if (s[i] == ')' && stk.top() == '(') {
                stk.pop();
            } else if (s[i] == ']' && stk.top() == '[') {
                stk.pop();
            } else if (s[i] == '}' && stk.top() == '{') {
                stk.pop();
            } else {
            return false;;
            }
        }
        return stk.empty();
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <stack>

using namespace std;

stack<char> stk;

bool isValid(string s) {
    for (int i = 0; i < s.size(); i++) {
        if (s[i] == '(' || s[i] == '[' || s[i] == '{') {
            stk.push(s[i]);
            continue;
        }

        if (stk.empty() && (s[i] == ')' || s[i] == ']' || s[i] == '}')) return false;

        if (s[i] == ')' && stk.top() == '(') {
            stk.pop();
        } else if (s[i] == ']' && stk.top() == '[') {
            stk.pop();
        } else if (s[i] == '}' && stk.top() == '{') {
            stk.pop();
        } else {
            return false;;
        }
    }
    return stk.empty();
}

int main() {
    string s;
    cin >> s;
    cout << isValid(s) << endl;
    return 0;
}

21. 合并两个有序链表

合并两个有序链表

思路：
遍历一遍即可
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        auto dummy = new ListNode(-1);
        auto cur = dummy;
        while (list1 && list2) {
            if (list1->val < list2->val) {
                cur->next = list1;
                cur = cur->next;
                list1 = cur->next;
            } else {
                cur->next = list2;
                cur = cur->next;
                list2 = cur->next;
            }
        }
        if (list1) cur->next = list1;
        if (list2) cur->next = list2;
        return dummy->next;
    }
};

22. 括号生成

括号生成

思路：
左括号小于n，就可以加；右括号数量小于左括号数量则可以加
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<string> ans;

    // lc为左括号的数量，rc为右括号的数量
    void dfs(int n, int lc, int rc, string res) {
        if (lc == n && rc == n) {
            ans.push_back(res);
            return;
        }
        if (lc < n) dfs(n, lc + 1, rc, res + '(');
        if (rc < lc) dfs(n, lc, rc + 1, res + ')');
    }

    vector<string> generateParenthesis(int n) {
        dfs(n, 0, 0, "");
        return ans;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <vector>

using namespace std;

vector<string> ans;

// lc为左括号的数量，rc为右括号的数量
void dfs(int n, int lc, int rc, string res) {
    if (lc == n && rc == n) {
        ans.push_back(res);
        return;
    }
    if (lc < n) dfs(n, lc + 1, rc, res + '(');
    if (rc < lc) dfs(n, lc, rc + 1, res + ')');
}

vector<string> generateParenthesis(int n) {
    dfs(n, 0, 0, "");
    return ans;
}

int main() {
    int n;
    cin >> n;
    vector<string> ans = generateParenthesis(n);
    for (auto s : ans) {
        cout << s << ' ';
    }
    cout << endl;
    return 0;
}

23. 合并K个升序链表

23. 合并K个升序链表

思路：归并，堆，优先队列，重载小于号

时间复杂度：knlogk

优先队列定义：priority_queue<Type, Container, Functional>

for (auto l : lists) if (l) heap.push(l); 优先队列 只是把 每个链表的头结点的地址 push进去了，而不是把整个链表 push进去。

因为优先队列中存的是 链表头结点的地址, 我们要比较的是结点的值 而不是 地址，所以 要自己定义 Cmp 比较 结点的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    // 重载 "()" 是因为 STL容器 在比较的时候用的是 结构体的小括号运算符
    struct Cmp {
        bool operator() (ListNode* a, ListNode* b) {
            return a->val > b->val; // 小根堆 是 '>'
        }
    };

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        // 优先队列 定义：priority_queue<Type, Container, Functional>
        // 因为 优先队列中存的是 链表头结点的地址, 我们要比较的是结点的值 而不是 地址
        // 所以 要自己定义 Cmp 比较 结点的值
        priority_queue<ListNode*, vector<ListNode*>, Cmp> heap;
        auto dummy = new ListNode(-1);
        auto cur = dummy;

        for (auto l : lists) if (l) heap.push(l);
        while (!heap.empty()) {
            auto t = heap.top();
            heap.pop();

            if (t->next) heap.push(t->next);

            cur->next = t;
            cur = cur->next;
        }
        return dummy->next;
    }
};

24. 两两交换链表中的节点

两两交换链表中的节点

思路：
用临时变量temp储存下一个值，方便调换
然后用before存储上一个值
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
        if (!head) return head;
        ListNode* h;
        if (head->next) h = head->next;
        else return head;
        ListNode* before = head;
        for (auto p = head; p && p->next; p = p->next) {
            auto temp = p->next;
            before->next = temp;
            p->next = temp->next;
            temp->next = p;
            before = p;
        }
        return h;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <vector>

using namespace std;

struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

ListNode* swapPairs(ListNode* head) {
    if (!head) return head;
    ListNode* h;
    if (head->next) h = head->next;
    else return head;
    ListNode* before = head;
    for (auto p = head; p && p->next; p = p->next) {
        auto temp = p->next;
        before->next = temp;
        p->next = temp->next;
        temp->next = p;
        before = p;
    }
    return h;
}

int main() {
    int k;
    auto dummy = new ListNode(-1);
    auto cur = dummy;
    while (cin >> k, k != -1) {
        cur->next = new ListNode(k);
        cur = cur->next;
    }
    auto head = swapPairs(dummy->next);
    for (auto i = head; i; i = i->next) {
        cout << i->val << ' ';
    }
    cout << endl;
    return 0;
}

25. K 个一组翻转链表

25. K 个一组翻转链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        auto dummy = new ListNode(-1);
        dummy->next = head;
        for (auto p = dummy; ;) {
            auto q = p;
            // 看看后面有没有k个结点
            for (int i = 0; i < k && p; i++, p = p->next);
            if (!p) break;

            // 反转内部
            auto a = q->next, b = a->next;
            for (int i = 0; i < k - 1; i++) {
                auto c = b->next;
                b->next = a;
                a = b, b = c;
            }

            // 反转外部
            auto t = q->next;
            q->next = a;
            t->next = b;
            p = t;
        }
        return dummy->next;
    }
};

26. 删除有序数组中的重复项

删除有序数组中的重复项

思路：
双指针
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int k = 0;
        for (int i = 0; i < nums.size(); i++) {
            if (!i || nums[i] != nums[i - 1]) {
                nums[k++] = nums[i];
            }
        }
        return k;
    }
};

27. 移除元素

移除元素

思路：
双指针
时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int k = 0;
        for (int i = 0; i < nums.size(); i++) {
            if (nums[i] != val) {
                nums[k++] = nums[i];
            }
        }
        return k;
    }
};

28. 实现 strStr()

实现 strStr()

思路：
kmp算法
时间复杂度：O(n + m)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int strStr(string s, string p) {
        if (p.empty()) return 0;
        int n = s.size(), m = p.size();
        // 字符串先补成从1开始
        s = ' ' + s, p = ' ' + p;

        vector<int> next(m + 1);
        // 求next数组，为什么从 i = 2 开始呢，因为 next[1] = 0
        // next 指的是非平凡的前缀和后缀相等的最大值，不包括本身，所以 next[1] = 0
        for (int i = 2, j = 0; i <= m; i++) {
            while (j && p[i] != p[j + 1]) j = next[j];
            if (p[i] == p[j + 1]) j++;
            next[i] = j;
        }

        for (int i = 1, j = 0; i <= n; i++) {
            while (j && s[i] != p[j + 1]) j = next[j];
            if (s[i] == p[j + 1]) j++;
            if (j == m) return i - m;
        }
        return -1;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
#include <vector>

using namespace std;

int strStr(string s, string p) {
    if (p.empty()) return 0;
    int n = s.size(), m = p.size();
    // 字符串先补成从1开始
    s = ' ' + s, p = ' ' + p;

    vector<int> next(m + 1);
    // 求next数组，为什么从 i = 2 开始呢，因为 next[1] = 0
    // next 指的是非平凡的前缀和后缀相等的最大值，不包括本身，所以 next[1] = 0
    for (int i = 2, j = 0; i <= m; i++) {
        while (j && p[i] != p[j + 1]) j = next[j];
        if (p[i] == p[j + 1]) j++;
        next[i] = j;
    }

    for (int i = 1, j = 0; i <= n; i++) {
        while (j && s[i] != p[j + 1]) j = next[j];
        if (s[i] == p[j + 1]) j++;
        if (j == m) return i - m;
    }
    return -1;
}

int main() {
    string s, p;
    cin >> s >> p;
    cout << strStr(s, p) << endl;
    return 0;
}

29. 两数相除

两数相除

思路：
快速幂+位运算
时间复杂度：O(log2n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int divide(int x, int y) {
        typedef long long LL;
        vector<LL> exp;
        bool is_minus = false;
        if (x > 0 && y < 0 || x < 0 && y > 0) is_minus = true;
        LL a = abs((LL)x), b = abs((LL)y);
        for (LL i = b; i <= a; i = i + i) exp.push_back(i);

        LL res = 0;
        for (int i = exp.size() - 1; i >= 0; i--) {
            if (a >= exp[i]) {
                a -= exp[i];
                res += 1LL << i;
            }
        }
        if (is_minus) res = -res;
        if (res > INT_MAX || res < INT_MIN) res = INT_MAX;
        return res;
    }
};

30. 串联所有单词的子串

30. 串联所有单词的子串

我们就可以枚举每个序列，对于每个序列我们可以用双指针来搜索包含words所有单词的连续序列。这里是以单词为单位进行双指针移动。

我们每次将窗口右端的单词加入哈希表，如果它的个数大于words中的个数，当前序列肯定不合法，我们不断地移动左端点使得窗口再次合法，当窗口长度为m时说明我们找到了一个答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    vector<int> findSubstring(string s, vector<string>& words) {
        if (words.empty()) return vector<int>();
        unordered_map<string, int> hash;
        for (auto &word : words) hash[word] ++ ;

        vector<int> res;
        int w = words[0].size(), n = words.size();
        for (int i = 0; i < w; i ++ ) {
            // 将序列切出来
            vector<string> ws;
            int j = i;
            while (j + w - 1 < s.size()) {
                ws.push_back(s.substr(j, w));
                j += w;
            }
            // 双指针匹配
            unordered_map<string, int> h;
            for (int a = 0, b = 0; b < ws.size(); b ++ ) {
                h[ws[b]] ++ ;
                while (h[ws[b]] > hash[ws[b]]) {
                    h[ws[a]] -- ;
                    a ++ ;
                }
                // 这里下标应为第i个序列的第a个单词
                if (b - a + 1 == n) res.push_back(i + a * w);
            }
        }
        return res;
    }
};

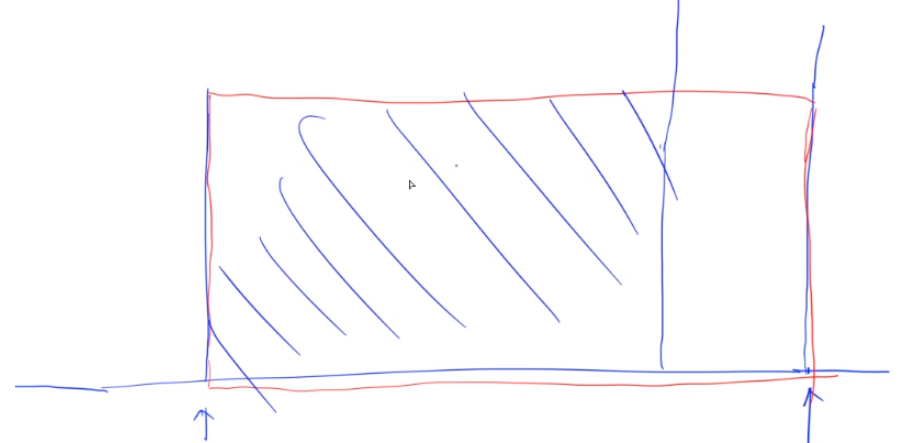
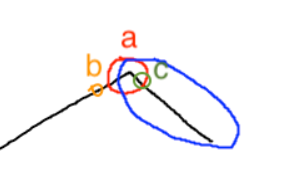
31. 下一个排列

下一个排列

思路：

首先逆序扫描一遍数组，找到降序的点（即：图中红色的点）
如图：

1

1
2
int k = nums.size();
while (k > 0 && nums[k - 1] >= nums[k]) k --;

循环结束k的值表示红色的点a的下标。

然后重新逆序遍历，找到最小的比k - 1大的点。由于在图中点a后面的点本身就是排好序了的，所以我们逆序遍历，第一个比k - 1大的点就是最小的比k - 1大的点。

1
2
int t = nums.size() - 1;
        while (nums[t] <= nums[k - 1]) t--;

然后交换这两个点

1
swap(nums[t], nums[k - 1]);

最后将后面（蓝色圈出来部分）下降的折线 捋成上升的形状。

1
reverse(nums.begin() + k, nums.end());

时间复杂度：O(n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int k = nums.size() - 1;
        while (k > 0 && nums[k - 1] >= nums[k]) k--;
        if (k == 0) {
            reverse(nums.begin(), nums.end());
        } else {
            int t = nums.size() - 1;
            while (nums[t] <= nums[k - 1]) t--;
            swap(nums[t], nums[k - 1]);
            reverse(nums.begin() + k, nums.end());
        }
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> nums;

void nextPermutation(vector<int>& nums) {
    int k = nums.size() - 1;
    while (k > 0 && nums[k - 1] >= nums[k]) k--;
    if (k == 0) {
        reverse(nums.begin(), nums.end());
    } else {
        int t = nums.size() - 1;
        while (nums[t] <= nums[k - 1]) t--;
        swap(nums[t], nums[k - 1]);
        reverse(nums.begin() + k, nums.end());
    }
}

int main() {
    int n;
    while (cin >> n, n != -1) {
        nums.push_back(n);
    }
    nextPermutation(nums);
    for (int i : nums) {
        cout << i << ' ';
    }
    cout << endl;
    return 0;
}

32. 最长有效括号

32. 最长有效括号

栈

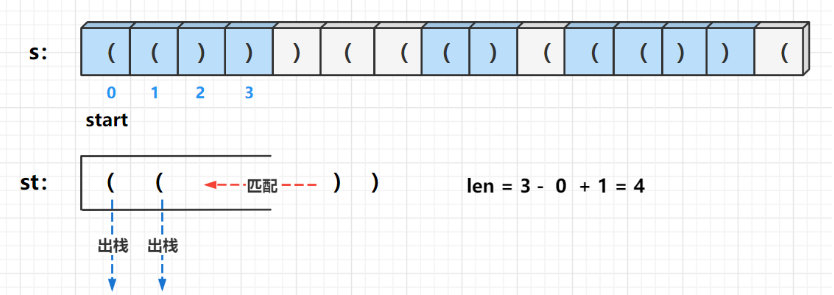
1、用栈维护当前待匹配的左括号的位置，同时用 start 记录一个新的可能合法的子串的起始位置，初始设为0。

2、如果s[i] ==’(‘，那么把i进栈。

3、如果s[i] == ‘)’,那么弹出栈顶元素 （代表栈顶的左括号匹配到了右括号），出栈后：

如果栈为空，说明以当前右括号为右端点的合法括号序列的左端点为start，则更新答案 i - start + 1。

如果栈不为空，说明以当前右括号为右端点的合法括号序列的左端点为栈顶元素的下一个元素，则更新答案i - stk.top() 。

4、遇到右括号)且当前栈为空，则当前的 start 开始的子串不再可能为合法子串了，下一个合法子串的起始位置可能是 i + 1，更新 start = i + 1。

实现细节：栈保存的是下标，总之一句话，栈中不可能保存右括号。

时间复杂度： 每个位置遍历一次，最多进栈一次，故时间复杂度为 O(n)。

image-20220813233749996

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int longestValidParentheses(string s) {
        stack<int> stk;
        int start = 0, ans = 0;
        for (int i = 0; i < s.size(); i++) {
            if (s[i] == '(') stk.push(i); // 左括号入栈   
            else {
                if (stk.size()) {
                    stk.pop(); // 匹配成功
                    if (stk.empty()) ans = max(ans, i - start + 1);
                    else ans = max(ans, i - stk.top());
                } else {
                    start = i + 1; // 更新可能的起点 
                }
            }
        }
        return ans;
    }
};

33. 搜索旋转排序数组

搜索旋转排序数组

思路：

二分找出分界点

1

时间复杂度：O(log2n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int search(vector<int>& nums, int target) {
    int l = 0, r = nums.size() - 1;
    if (nums[l] > nums[r]) {
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] >= nums[0]) l = mid + 1;
            else r = mid;
        }

        if (nums[0] <= target) l = 0, r = r - 1;
        else r = nums.size() - 1;

    }
    while (l < r) {
        int mid = l + r + 1 >> 1;
        if (nums[mid] > target) r = mid - 1;
        else l = mid;
    }
    if (nums[l] == target) return l;
    return -1;
}

34. 在排序数组中查找元素的第一个和最后一个位置

在排序数组中查找元素的第一个和最后一个位置

思路：

两次二分即可

时间复杂度：O(log2n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if (nums.empty()) return {-1, -1};
        vector<int> ans;
        int l = 0, r = nums.size() - 1;
        while (l < r) {
            int mid = (l + r) >> 1;
            if (nums[mid] < target) {
                l = mid + 1;
            } else {
                r = mid;
            }
        }
        if (nums[l] != target) return {-1, -1};

        ans.push_back(r);

        l = 0, r = nums.size() - 1;
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (nums[mid] > target) {
                r = mid - 1;
            } else {
                l = mid;
            }
        }
        ans.push_back(r);
        return ans;
    }
};

35. 搜索插入位置

搜索插入位置

思路：

二分

时间复杂度：O(log2n)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int l = 0, r = nums.size() - 1;
        int mid;
        while (l < r) {
            mid = l + r >> 1;
            if (nums[mid] < target) {
                l = mid + 1;
            } else {
                r = mid;
            }
        }
        if (l == nums.size() - 1 && target > nums[l]) l++;
        return l;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <bits/stdc++.h>

using namespace std;

int searchInsert(vector<int>& nums, int target) {
    int l = 0, r = nums.size() - 1;
    int mid; 
    while (l < r) {
    	mid = l + r >> 1;
    	if (nums[mid] < target) {
    		l = mid + 1;
    	} else {
    		r = mid;
    	}
    }
    if (l == nums.size() - 1 && target > nums[l]) l++;
    return l;
}

int main() {
	vector<int> nums = {1};
	int target = 0;
	cout << searchInsert(nums, target) << endl;
	return 0;
}

36. 有效的数独

有效的数独

时间复杂度：O(n2)
核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        // res[9]为行，col[9]为列
        int res[9], col[9];
        for (int i = 0; i < 9; i++) {
            memset(res, 0, sizeof res);
            memset(col, 0, sizeof col);
            for (int j = 0; j < 9; j++) {
                if (board[i][j] != '.' && ++res[board[i][j] - '1'] > 1) return false;
                if (board[j][i] != '.' && ++col[board[j][i] - '1'] > 1) return false;
            }
        }

        // res[9]为九宫格
        int rc[9] = {0};
        for (int i = 0; i < 9; i += 3) {
            for (int j = 0; j < 9; j += 3) {
                memset(rc, 0, sizeof rc);
                for (int x = 0; x < 3; x++) {
                    for (int y = 0; y < 3; y++) {
                        if (board[x + i][y + j] != '.' && ++rc[board[x + i][y + j] - '1'] > 1) return false;
                    }
                }
            }
        }
        
        return true;
    }
};

37. 解数独

37. 解数独

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    // 记录行，列，小方块中1-9有没有重复
    bool row[9][9], col[9][9], cell[3][3][9];

    bool dfs(vector<vector<char>>& board, int x, int y) {
        // 换行
        if (y == 9) x++, y = 0;
        // 九宫格遍历完了
        if (x == 9) return true;

        // 如果这里本来就有数，就自动跳到下一个
        if (board[x][y] != '.') return dfs(board, x, y + 1);

        for (int i = 0; i < 9; i++) {
            // 行，列，九宫格都没有重复，就可以递归下去
            if (!row[x][i] && !col[y][i] && !cell[x / 3][y / 3][i]) {
                board[x][y] = '1' + i;
                row[x][i] = col[y][i] = cell[x / 3][y / 3][i] = true;
                if (dfs(board, x, y + 1)) return true;
                // 全局变量要恢复现场
                board[x][y] = '.';
                row[x][i] = col[y][i] = cell[x / 3][y / 3][i] = false;
            }
        }
        return false;
    }

    void solveSudoku(vector<vector<char>>& board) {
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] != '.') {
                    int t = board[i][j] - '1';
                    row[i][t] = col[j][t] = cell[i / 3][j / 3][t] = true;
                }
            }
        }

        int x = 0, y = 0;
        dfs(board, x, y);
    }
};

38. 外观数列

外观数列

思路：

简单模拟一下即可，双指针

时间复杂度：O(n)

核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    string countAndSay(int n) {
        string s = "1";
        for (int i = 0; i < n - 1; i++) {
            string t;
            for (int k = 0, j = k; j < s.size();) {
                while (j < s.size() && s[j] == s[k]) {
                    j++;
                }
                t += to_string(j - k) + s[k];
                k = j;
            }
            s = t;
        }
        return s;
    }
};

39. 组合总和

组合总和

思路：

暴力枚举每个数选几个

核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:

    vector<vector<int>> ans;
    vector<int> path;

    vector<vector<int>> combinationSum(vector<int> &c, int target) {
        dfs(c, 0, target);
        return ans;
    }

    void dfs(vector<int> &c, int u, int target) {
        if (target == 0) {
            ans.push_back(path);
            return;
        }
        if (u == c.size()) return;

        for (int i = 0; c[u] * i <= target; i++) {
            dfs(c, u + 1, target - c[u] * i);
            path.push_back(c[u]);
        }

        // 恢复现场
        for (int i = 0; c[u] * i <= target; i++) {
            path.pop_back();
        }
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
#include <vector>

using namespace std;

class Solution {
public:

    vector<vector<int>> ans;
    vector<int> path;

    vector<vector<int>> combinationSum(vector<int> &c, int target) {
        dfs(c, 0, target);
        return ans;
    }

    void dfs(vector<int> &c, int u, int target) {
        if (target == 0) {
            ans.push_back(path);
            return;
        }
        if (u == c.size()) return;

        for (int i = 0; c[u] * i <= target; i++) {
            dfs(c, u + 1, target - c[u] * i);
            path.push_back(c[u]);
        }

        // 恢复现场
        for (int i = 0; c[u] * i <= target; i++) {
            path.pop_back();
        }
    }
};

int main() {
    vector<int> c = {2,3,5};
    int target = 8;
    Solution s;
    vector<vector<int>> ans = s.combinationSum(c, target);
    for (int i = 0; i < ans.size(); i++) {
        for (int j = 0; j < ans[i].size(); j++) {
            cout << ans[i][j] << ' ';
        }
        cout << endl;
    }
    cout << endl;
    return 0;
}

40. 组合总和 II

组合总和 II

思路：

先求每个数最多能出现的次数，然后枚举每个数选几个，并且加上个数限制即可

核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:

    vector<vector<int>> ans;
    vector<int> path;

    vector<vector<int>> combinationSum2(vector<int> &c, int target) {
        sort(c.begin(), c.end());
        dfs(c, 0, target);
        return ans;
    }

    void dfs(vector<int> &c, int u, int target) {
        if (target == 0) {
            ans.push_back(path);
            return;
        }
        if (u == c.size()) return;

        int k = u + 1;
        while (k < c.size() && c[k] == c[u]) k++;
        int cnt = k - u;

        for (int i = 0; c[u] * i <= target && i <= cnt; i++) {
            dfs(c, k, target - c[u] * i);
            path.push_back(c[u]);
        }

        // 恢复现场
        for (int i = 0; c[u] * i <= target && i <= cnt; i++) {
            path.pop_back();
        }
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

class Solution {
public:

    vector<vector<int>> ans;
    vector<int> path;

    vector<vector<int>> combinationSum2(vector<int> &c, int target) {
        sort(c.begin(), c.end());
        dfs(c, 0, target);
        return ans;
    }

    void dfs(vector<int> &c, int u, int target) {
        if (target == 0) {
            ans.push_back(path);
            return;
        }
        if (u == c.size()) return;

        int k = u + 1;
        while (k < c.size() && c[k] == c[u]) k++;
        int cnt = k - u;

        for (int i = 0; c[u] * i <= target && i <= cnt; i++) {
            dfs(c, k, target - c[u] * i);
            path.push_back(c[u]);
        }

        // 恢复现场
        for (int i = 0; c[u] * i <= target && i <= cnt; i++) {
            path.pop_back();
        }
    }
};

int main() {
    vector<int> c = {2,3,5};
    int target = 8;
    Solution s;
    vector<vector<int>> ans = s.combinationSum(c, target);
    for (int i = 0; i < ans.size(); i++) {
        for (int j = 0; j < ans[i].size(); j++) {
            cout << ans[i][j] << ' ';
        }
        cout << endl;
    }
    cout << endl;
    return 0;
}

41. 缺失的第一个正数

缺失的第一个正数

思路一：

自己设计哈希

将数组中所有小于等于 0 的数修改为 N+1；

遍历数组中的每一个数 x，它可能已经被打了标记，因此原本对应的数为 ∣x∣。如果∣x∣∈[1,N]，那么我们给数组中的第 ∣x∣−1 个位置的数添加一个负号。如果它已经有负号，不需要重复添加；

在遍历完成之后，如果数组中的每一个数都是负数，那么答案是 N+1，否则答案是第一个正数的位置加 1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int firstMissingPositive(vector<int>& nums) {
        int n = nums.size();
        for (int& i : nums) 
            if (i <= 0) 
                i = n + 1;
        
        for (int i = 0; i < n; i++) {
            int num = abs(nums[i]);
            if (num <= n)
                nums[num - 1] = -abs(nums[num - 1]);
        }

        for (int i = 0; i < n; i++)
            if (nums[i] > 0)
                return i + 1;

        return n + 1;
    }
};

思路二：

原地哈希算法：

原地哈希算法主要应用在范围为 [0, len(nums)] 的数组解法中，将数组元素本身作为nums 的下标，即 nums[nums[i]]

原地哈希映射：保证1出现在nums[0]的位置上，2出现在nums[1]的位置上，…，n出现在nums[n-1]的位置上，其他的数字不管。例如[3,4,-1,1]将被排序为[1,-1,3,4]

遍历nums，找到第一个不在应在位置上的1到n的数。例如，排序后的[1,-1,3,4]中第一个 nums[i] != i + 1 的是数字2（注意此时i=1）。

时间复杂度分析：代码中第二层while循环，每循环一次，会将一个数放在正确的位置上，所以总共最多执行 n 次，所以总时间复杂度 O(n)。

时间复杂度：O(n)

空间复杂度：O(1)

核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int firstMissingPositive(vector<int>& nums) {
        int n = nums.size();
        for (int i = 0; i < n; i++) {
            while (nums[i] > 0 && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {
                swap(nums[nums[i] - 1], nums[i]);
            }
        }
        for (int i = 0; i < n; i++) {
            if (nums[i] != i + 1) {
                return i + 1;
            }
        }
        return n + 1;
    }
};

42. 接雨水

42. 接雨水

算height[i]两边的高度取个min 然后跟h[i]做个差就是h[i]能存的水

时间复杂度：O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size(), res = 0;
        vector<int> left(n), right(n);
        left[0] = height[0];
        right[n - 1] = height[n - 1];
        for (int i = 1; i < n; i++) {
            left[i] = max(left[i - 1], height[i]);
        }
        for (int i = n - 2; i >= 0; i--) {
            right[i] = max(right[i + 1], height[i]);
        }
        for (int i = 1; i < n - 1; i++) {
            res += min(left[i], right[i] ) - height[i];
        }
        return res;
    }
};

43. 字符串相乘

字符串相乘

思路：

将A[i] * B[j] 加到 C[i + j] 里面，最后再一起进位

image-20220412220151895

时间复杂度：O(n)

核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    string multiply(string num1, string num2) {
        vector<int> A, B;
        int n = num1.size(), m = num2.size();
        for (int i = n - 1; i >= 0; i--) {
            A.push_back(num1[i] - '0');
        }
        for (int i = m - 1; i >= 0; i--) {
            B.push_back(num2[i] - '0');
        }
        vector<int> C(n + m);
        // 将A[i] * B[j] 加到 C[i + j] 里面
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                C[i + j] += A[i] * B[j];
            }
        }
        // 处理进位
        for (int i = 0, t = 0; i < C.size(); i++) {
            t += C[i];
            C[i] = t % 10;
            t /= 10;
        }
        // 去除前导0
        int k = C.size() - 1;
        while (k > 0 && C[k] == 0) k--;
        // 数字转字符串
        string ans;
        while (k >= 0) ans += C[k--] + '0';
        return ans;
    }
};

ACM模式代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
#include <vector>
using namespace std;

string multiply(string num1, string num2) {
    vector<int> A, B;
    int n = num1.size(), m = num2.size();
    for (int i = n - 1; i >= 0; i--) {
        A.push_back(num1[i] - '0');
    }
    for (int i = m - 1; i >= 0; i--) {
        B.push_back(num2[i] - '0');
    }
    vector<int> C(n + m);
    // 将A[i] * B[j] 加到 C[i + j] 里面
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            C[i + j] += A[i] * B[j];
        }
    }
    // 处理进位
    for (int i = 0, t = 0; i < C.size(); i++) {
        t += C[i];
        C[i] = t % 10;
        t /= 10;
    }
    // 去除前导0
    int k = C.size() - 1;
    while (k > 0 && C[k] == 0) k--;
    // 数字转字符串
    string ans;
    while (k >= 0) ans += C[k--] + '0';
    return ans;
}

int main() {
    string num1, num2;
    cin >> num1 >> num2;
    cout << multiply(num1, num2) << endl;
    return 0;
}

44. 通配符匹配

44. 通配符匹配

dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool isMatch(string s, string p) {
        int n = s.size(), m = p.size();
        s = ' ' + s, p = ' ' + p;
        vector<vector<bool>> f(n + 1, vector<bool>(m + 1));
        f[0][0] = true;
        for (int i = 0; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (p[j] == '*') f[i][j] = i && f[i - 1][j] || f[i][j - 1];
                else f[i][j] = (s[i] == p[j] || p[j] == '?') && i && f[i - 1][j - 1];
            }
        }
        return f[n][m];
    }
};

45. 跳跃游戏 II

跳跃游戏 II

思路一：动态规划

定义f[i]为跳到点i需要的最小步数

时间复杂度：O(n2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int jump(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n, 0x3f3f3f3f);
        f[0] = 0; // 0跳到自己就是0
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < i; j++) {
                // 只要前面的点能跳到i点就更新最小值
                if (j + nums[j] >= i) {
                    f[i] = min(f[j] + 1, f[i]);
                }
            }
        }
        return f[n - 1];
    }
};

思路二：

动态规划+贪心

  1. 设状态 f(i) 表示到达 i 所需要的最少步数。

  2. f(0)=0，其余待定。定义辅助指针 last 为第一次到达 i 时上一步的位置，last 从 0 开始。

  3. 我们会发现f[i]是具有单调性的，也就是f[i + 1] >= f[i]。

  4. 根据以上得知，令 f(i)=f(last)+1 后，f(i) 就会是最优值。

    在动态规划时瓶颈就在于更新每个点的最小值时需要遍历所有能跳到i的点，而有了单调性以后就可以用第一个能跳到i的点更新了，这里无论是取哪一个点跳到i，其最终的结果是一样的，但是取第一个点和取最后一个点所需要的步数可能不相同，所以尽量选择靠前的点，这样步数就可能会减少，贪心的思想。

  5. 故可以根据 i 来让last 向后移动，找到最早的可以一步到达 i 的位置，然后根据 f(last) 更新 f(i)。

时间复杂度：O(n)

核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int jump(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n);
        for (int i = 1, last = 0; i < n; i++) {
            // 根据i来更新last。如果last + nums[last]够不到i，那就往后移last
            while (last + nums[last] < i) last++;
            // 根据f[last]更新f[i]，last可以一步走到i
            f[i] = f[last] + 1;
        }
        return f[n - 1];
    }
};

46. 全排列

全排列

思路一：

next_permutation函数

时间复杂度：O(n x n!)

核心代码：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> ans;
        do {
            ans.push_back(nums);
        } while (next_permutation(nums.begin(), nums.end()));
        return ans;
    }
};

思路二：

时间复杂度：O(n x n!)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<vector<int>> ans;
    vector<bool> st;
    void dfs(vector<int>& nums, int u, vector<int>& res) {
        if (u == nums.size()) {
            ans.push_back(res);
            return;
        }

        for (int i = 0; i < nums.size(); i++) {
            if (!st[i]) {
                res.push_back(nums[i]);
                st[i] = true;
                dfs(nums, u + 1, res);
                st[i] = false;
                res.pop_back();
            }
        }
    }

    vector<vector<int>> permute(vector<int>& nums) {
        for (int i = 0; i < nums.size(); i ++ ) st.push_back(false);
        vector<int> res;
        dfs(nums, 0, res);
        return ans;
    }
};

47. 全排列 II

47. 全排列 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<vector<int>> ans;
    vector<bool> st;
    void dfs(vector<int>& nums, int u, vector<int>& res) {
        if (u == nums.size()) {
            ans.push_back(res);
            return;
        }

        for (int i = 0; i < nums.size(); i++) {
            if (!st[i]) {
                if (i && nums[i - 1] == nums[i] && !st[i - 1]) continue;
                res.push_back(nums[i]);
                st[i] = true;
                dfs(nums, u + 1, res);
                st[i] = false;
                res.pop_back();
            }
        }
    }

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        for (int i = 0; i < nums.size(); i ++ ) st.push_back(false);
        vector<int> res;
        dfs(nums, 0, res);
        return ans;
    }
};

48. 旋转图像

先沿着左对角线交换，然后沿着中线，左右交换

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        for (int i = 0; i < matrix.size(); i++)
            for (int j = 0; j < i; j++) 
                swap(matrix[i][j], matrix[j][i]);

        for (int i = 0; i < matrix.size(); i++)
            for (int j = 0, k = matrix.size() - 1; j < k; j++, k--) 
                swap(matrix[i][j], matrix[i][k]);
    }
};

49. 字母异位词分组

49. 字母异位词分组

哈希表+分组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        vector<vector<string>> ans;
        unordered_map<string, vector<string>> hash;
        for (int i = 0; i < strs.size(); i++) {
            auto tmp = strs[i];
            sort(tmp.begin(), tmp.end());
            hash[tmp].push_back(strs[i]);
        }
        for (auto& it : hash) ans.push_back(it.second);
        return ans;
    }
};

50. Pow(x, n)

快速幂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    double myPow(double x, int n) {
        typedef long long LL;
        bool is_minus = n < 0;
        double res = 1;
        for (LL k = abs(LL(n)); k; k >>= 1) {
            if (k & 1) res *= x;
            x *= x;
        }
        if (is_minus) res = 1 / res;
        return res;
    }
};

51. N 皇后

dfs+回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    vector<vector<string>> ans;
    vector<bool> col, dg, udg;
    vector<string> path;
    int n;

    void dfs(int u) {
        if (u == n) {
            ans.push_back(path);
            return;
        }
        for (int i = 0; i < n; i++) {
            if (!col[i] && !dg[u - i + n] && !udg[u + i]) {
                path[u][i] = 'Q';
                col[i] = dg[u - i + n] = udg[u + i] = true;
                dfs(u + 1);
                path[u][i] = '.';
                col[i] = dg[u - i + n] = udg[u + i] = false;
            }
        }
    }

    vector<vector<string>> solveNQueens(int _n) {
        n = _n;
        col = vector<bool>(n);
        dg = udg = vector<bool>(2 * n);
        path = vector<string>(n, string(n, '.'));
        dfs(0);
        return ans;
    }
};

52. N 皇后 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    int n;
    vector<bool> col, dg, udg;
    vector<string> path;
    int sum = 0;

    void dfs(int u) {
        if (u == n) {
            sum++;
            return;
        }
        for (int i = 0; i < n; i++) {
            if (!col[i] && !dg[u - i + n] && !udg[u + i]) {
                path[u][i] = 'Q';
                col[i] = dg[u - i + n] = udg[u + i] = true;
                dfs(u + 1);
                path[u][i] = '.';
                col[i] = dg[u - i + n] = udg[u + i] = false;
            }
        }
    }

    int totalNQueens(int _n) {
        n = _n;
        col = vector<bool>(n);
        dg = udg = vector<bool>(2 * n);
        path = vector<string>(n, string(n, '.'));
        dfs(0);
        return sum;
    }
};

53. 最大子数组和

dp

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int res = INT_MIN;
        for (int i = 0, last = 0; i < nums.size(); i++) {
            last = nums[i] + max(last, 0);
            res = max(res, last);
        }
        return res;
    }
};

54. 螺旋矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> ans;
        int n = matrix.size(), m = matrix[0].size();
        vector<vector<bool>> st(n + 1, vector<bool>(m + 1, false));
        int dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0};
        for (int i = 0, x = 0, y = 0, d = 0; i < n * m; i++) {
            st[x][y] = true;
            ans.push_back(matrix[x][y]);

            int a = x + dx[d], b = y + dy[d];
            if (a < 0 || a >= n || b < 0 || b >= m || st[a][b]) {
                d = (d + 1) % 4;
                a = x + dx[d], b = y + dy[d];
            }
            x = a, y = b;
        }
        return ans;
    }
};

55. 跳跃游戏

贪心

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool canJump(vector<int>& nums) {
        // i是当前的位置，j是能跳到最远的位置
        for (int i = 0, j = 0; i < nums.size(); i++) {
            // 如果j < i，说明从之前的点跳不到i
            if (j < i) return false;
            // 更新能跳到最远的点
            j = max(j, i + nums[i]);
        }
        // 如果全部遍历完了，说明可以跳到最后一个点
        return true;
    }
};

56. 合并区间

对vector使用sort函数排序，自动就是按照第一个关键字排序，然后再是第二个。。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& a) {
        vector<vector<int>> ans;
        sort(a.begin(), a.end());
        int l = a[0][0], r = a[0][1];
        for (int i = 1; i < a.size(); i++) {
            if (a[i][0] > r) {
                ans.push_back({l, r});
                l = a[i][0], r = a[i][1];
            } else {
                r = max(r, a[i][1]);   
            }  
        } 
        ans.push_back({l, r}); 
        return ans;
    }
};

57. 插入区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<vector<int>> insert(vector<vector<int>>& a, vector<int>& b) {
        vector<vector<int>> ans;
        int i = 0;
        // 完全没交集的区间
        while (i < a.size() && a[i][1] < b[0]) ans.push_back(a[i++]);
        // 有交集的区间合并
        if (i < a.size()) {
            // 定义左端点
            b[0] = min(a[i][0], b[0]);
            // 更新右端点
            while (i < a.size() && a[i][0] <= b[1]) b[1] = max(b[1], a[i++][1]);
        }
        ans.push_back(b);
        while (i < a.size()) ans.push_back(a[i++]);
        return ans;
    }
};

58. 最后一个单词的长度

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int lengthOfLastWord(string s) {
        int i = s.size() - 1;
        while (i >= 0 && s[i] == ' ') i--;
        int r = i;
        while (i >= 0 && s[i] != ' ') i--;
        return r - i;
    }
};

59. 螺旋矩阵 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> ans(n, vector<int>(n, 0));
        int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
        for (int i = 0, x = 0, y = 0, d = 0; i < n * n; i++) {
            ans[x][y] = i + 1;

            int a = x + dx[d], b = y + dy[d];
            if (a < 0 || a >= n || b < 0 || b >= n || ans[a][b]) {
                d = (d + 1) % 4;
                a = x + dx[d], b = y + dy[d];
            }
            x = a, y = b;
        }
        return ans;
    }
};

60. 排列序列

模拟题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <vector>

using namespace std;

string getPermutation(int n, int k) {
    // 预处理阶乘
    vector<int> fact(n + 1);
    // 0的阶乘是1
    fact[0] = 1;
    int s = 1;
    for (int i = 1; i <= n; i++) {
        s *= i;
        fact[i] = s;
    }

    vector<bool> st(n);
    string res;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (!st[j]) {
                if (fact[n - i] < k) k -= fact[n - i];
                else {
                    res += to_string(j);
                    st[j] = true;
                    break;
                }
            }
        }
    }
    return res;
}

int main() {
    int n = 3, k = 3;
    cout << getPermutation(n, k) << endl;
    return 0;
}

61. 旋转链表

链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
        if (k == 0) return head;
        if (!head) return head;
        // 节点的个数
        int num = 0;
        for (auto p = head; p; p = p->next) num++;
        k = k % num;

        auto dummy = new ListNode(-1000);
        dummy->next = head;
        int a = 0;
        auto p = dummy;
        for (; a < num - k; p = p->next, a++);
        

        auto cur = dummy->next;

        dummy->next = p->next;
        p->next = nullptr;

        p = dummy;
        a = 0;
        for (; a < k; a++, p = p->next);

        p->next = cur;

        return dummy->next;
    }
};

62. 不同路径

dp

某个点的方案数等于左边和上边的方案数之和

image-20220919152208538 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
#include <vector>

using namespace std;

int uniquePaths(int m, int n) {
    vector<vector<int>> f (m, vector<int>(n));
    for (int i = 0; i < m; i++)
        for (int j = 0; j < n; j++)
            if (!i && !j) f[i][j] = 1;
            else {
                if (i) f[i][j] += f[i - 1][j];
                if (j) f[i][j] += f[i][j - 1];
            }
    return f[m - 1][n - 1];
}

int main() {
    int n = 3, k = 7;
    cout << uniquePaths(n, k) << endl;
    return 0;
}

63. 不同路径 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();

        vector<vector<int>> f(m, vector<int>(n));
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (!i && !j && obstacleGrid[i][j] != 1) f[i][j] = 1;
                else {
                    if (i && obstacleGrid[i][j] != 1) f[i][j] += f[i - 1][j];
                    if (j && obstacleGrid[i][j] != 1) f[i][j] += f[i][j - 1];
                }
            }
        }
        return f[m - 1][n - 1];
    }
};

64. 最小路径和

dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int n = grid.size();
        if (!n) return 0;
        int m = grid[0].size();

        vector<vector<int>> f(n, vector<int>(m, INT_MAX));

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (!i && !j) f[i][j] = grid[i][j];
                else {
                    if (i) f[i][j] = min(f[i][j], f[i - 1][j] + grid[i][j]);
                    if (j) f[i][j] = min(f[i][j], f[i][j - 1] + grid[i][j]);
                }
            }
        }
        return f[n - 1][m - 1];
    }
};

66. 加一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<int> plusOne(vector<int>& digits) {
        int n = digits.size() - 1;
        digits[n]++;
        while (n >= 0 && digits[n] == 10) {
            digits[n] = 0;
            if (n - 1 >= 0)
                digits[n - 1]++;
            n--;
        }
        vector<int> digits2;
        if (n == -1) {
            digits2.push_back(1);
            for (int i = 0; i < digits.size(); i++) {
                digits2.push_back(digits[i]);
            }
            return digits2;
        }
        return digits;
    }
};

67. 二进制求和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <algorithm>

using namespace std;

string addBinary(string a, string b) {
    if (a.size() > b.size()) return addBinary(b, a);
    reverse(a.begin(), a.end());
    reverse(b.begin(), b.end());
    int a_len = a.size(), b_len = b.size();

    int t = 0;
    string c;

    int i = 0, j = 0;
    for (; i < a_len; i++, j++) {
        t = a[i] - '0' + b[j] - '0' + t;
        if (t >= 2) {
            c += to_string(t % 2);
            t /= 2;
        } else {
            c += to_string(t);
            t = 0;
        }
    }
    for (; j < b_len; j++) {
        t = t + b[j] - '0';
        if (t >= 2) {
            c += to_string(t % 2);
            t /= 2;
        } else {
            c += to_string(t);
            t = 0;
        }
    }
    if (t) c += "1";
    reverse(c.begin(), c.end());
    return c;
}

int main() {
    string a = "100", b = "110010";
    cout << addBinary(a, b) << endl;
    return 0;
}

69. x 的平方根

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) return 0;
        if (x == 1) return 1;
        long long l = 1, r = x;
        long long m = (l + r >> 1);
        while (l - r > 1 || l - r < -1) {
            if (m <= x / m) l = m;
            else r = m;
            m = l + r >> 1;
        }
        return l;
    }
};
-------------本文结束感谢您的阅读-------------